Коэффициент детерминации является одним из основных показателей в статистике и регрессионном анализе. Он позволяет определить, насколько успешно модель регрессии объясняет изменения в зависимой переменной. В Excel коэффициент детерминации вычисляется с помощью функции R^2.
Коэффициент детерминации принимает значения от 0 до 1 и интерпретируется как доля объясненной вариации зависимой переменной. Значение 0 означает, что модель не объясняет никакую вариацию, а значение 1 означает, что модель полностью объясняет все наблюдаемые изменения. Чем выше значения коэффициента детерминации, тем лучше модель объясняет изменения в данных.
Для расчета коэффициента детерминации в Excel необходимо использовать функцию R^2. Эта функция принимает два аргумента: диапазон значений зависимой переменной и диапазон значений объясняющих переменных. После применения функции, Excel выдаст значение коэффициента детерминации.
Коэффициент детерминации в Excel является важным инструментом для анализа регрессионных моделей. Он позволяет оценить степень объяснения изменений в зависимой переменной и определить, насколько точны и предсказуемы полученные результаты. Использование функции R^2 в Excel позволяет проводить более глубокий анализ данных и принимать обоснованные решения на основе полученных результатов.
Что такое коэффициент детерминации в Excel?
Значение коэффициента детерминации варьируется от 0 до 1. Если R2 равен 0, это означает отсутствие связи между переменными. Если R2 равен 1, это означает, что все изменения в зависимой переменной могут быть объяснены изменениями в независимой переменной. Чем ближе значение R2 к 1, тем лучше модель объясняет зависимость между переменными.
Для расчета коэффициента детерминации в Excel необходимо сначала выполнить линейную регрессию с помощью функции ЛИНЕЙНАЯ( ) и сохранить прогнозные значения в отдельном столбце. Затем можно использовать функцию КОЭФФИЦИЕНТ.ДЕТЕРМИНАЦИИ( ), указав в аргументах диапазон фактических значений и диапазон прогнозных значений. Результатом будет значение коэффициента детерминации R2.
Коэффициент детерминации в Excel позволяет оценить качество линейной модели на основе имеющихся данных. Это полезный инструмент для анализа и прогнозирования зависимых переменных в экономике, финансах, науке и других областях.
Зачем нужен коэффициент детерминации?
Коэффициент детерминации принимает значения от 0 до 1, где 0 означает, что модель не объясняет никакой дисперсии зависимой переменной, а 1 говорит о том, что модель полностью объясняет всю дисперсию зависимой переменной. Таким образом, чем ближе значение коэффициента детерминации к 1, тем лучше модель соответствует наблюдаемым данным.
Значимость коэффициента детерминации
Коэффициент детерминации является важным показателем для определения качества модели. Он позволяет сравнить несколько различных моделей между собой и выбрать наиболее подходящую. Кроме того, данный коэффициент позволяет проверить статистическую значимость зависимости между переменными и определить, насколько предсказания модели согласуются с реальными наблюдениями.
Интерпретация коэффициента детерминации
Интерпретация коэффициента детерминации зависит от контекста и типа исследования. В некоторых случаях, даже небольшое значение коэффициента может оказаться статистически значимым и иметь практическую значимость. В других случаях, даже высокое значение коэффициента может не иметь практического применения, если модель не является пригодной для предсказания и объяснения зависимой переменной.
Какие данные необходимо иметь для расчета коэффициента детерминации?
Для расчета коэффициента детерминации в Excel необходимо иметь два набора данных: набор независимых переменных (X) и набор зависимых переменных (Y). В каждом наборе должно быть одинаковое количество значений, чтобы точно соответствовать друг другу.
Набор независимых переменных (X) обычно представляет собой факторы, которые мы считаем независимыми и могут влиять на значение зависимой переменной. Например, в случае изучения факторов, влияющих на успеваемость студентов, набор независимых переменных может включать такие факторы, как количество часов занятий, количество часов самостоятельного обучения и т.д.
Набор зависимых переменных (Y) представляет собой значение, которое мы пытаемся предсказать или объяснить с помощью набора независимых переменных. В нашем примере с успеваемостью студентов, набор зависимых переменных будет включать оценки, полученные этими студентами.
Пример:
Допустим, у нас есть данные о количестве часов самостоятельного обучения (X) и оценках (Y) для 10 студентов. Зная эти данные, мы можем рассчитать коэффициент детерминации, чтобы определить, насколько хорошо наши данные объясняют изменения в оценках студентов. Для расчета коэффициента детерминации в Excel будет использоваться формула R^2 = SSreg / SStot, где SSreg — сумма квадратов регрессии, а SStot — общая сумма квадратов.
| Номер студента | Количество часов самостоятельного обучения (X) | Оценка (Y) |
|---|---|---|
| 1 | 10 | 90 |
| 2 | 7 | 85 |
| 3 | 12 | 92 |
| 4 | 5 | 78 |
| 5 | 8 | 88 |
| 6 | 10 | 90 |
| 7 | 6 | 80 |
| 8 | 9 | 87 |
| 9 | 11 | 91 |
| 10 | 7 | 85 |
Используя эти данные, мы можем рассчитать коэффициент детерминации в Excel, чтобы определить, насколько хорошо наши данные объясняют изменения в оценках студентов.
Как рассчитать коэффициент детерминации в Excel?
- Откройте программу Excel и создайте два столбца данных – один для независимой переменной и один для зависимой переменной.
- Введите нужные значения в каждый столбец.
- Выберите ячейку, в которой хотите получить результат коэффициента детерминации.
- Введите формулу для расчета коэффициента детерминации, используя функцию R^2:
=R^2(независимый диапазон; зависимый диапазон)- Нажмите клавишу Enter, чтобы выполнить расчет.
Excel автоматически выполнит расчет и выведет значение коэффициента детерминации в выбранной ячейке. Коэффициент детерминации будет представлен в виде числа от 0 до 1, где 1 означает идеальное соответствие между переменными, а 0 означает отсутствие соответствия.
Рассчитывая коэффициент детерминации в Excel, вы можете получить представление о том, насколько хорошо модель регрессии описывает данные и какую долю вариации зависимой переменной можно объяснить с помощью независимой переменной.
Как интерпретировать значение коэффициента детерминации?
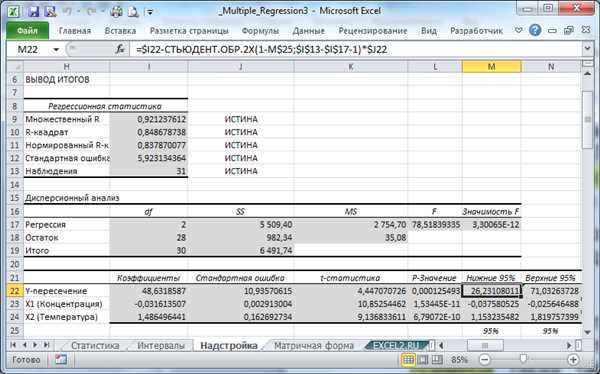
Значение коэффициента детерминации может находиться в диапазоне от 0 до 1, где 0 означает, что модель не объясняет вариацию зависимой переменной, а 1 — что модель полностью объясняет вариацию. В общем случае, чем ближе значение коэффициента детерминации к 1, тем лучше подходит модель к данным.
Однако интерпретация значения коэффициента детерминации может зависеть от контекста и конкретной задачи. Например, если мы рассматриваем модель, в которой зависимая переменная имеет сложное поведение и зависит от большого числа независимых переменных, то даже значение коэффициента детерминации около 0.5 может считаться хорошим результатом.
Чтобы более полно понять значение коэффициента детерминации, рекомендуется провести дополнительный анализ, такой как проверка статистической значимости коэффициента и оценка других метрик модели, таких как среднеквадратическая ошибка и средняя абсолютная ошибка.
| Значение коэффициента детерминации | Интерпретация |
|---|---|
| 0 — 0.2 | Модель имеет очень низкую предсказательную способность |
| 0.2 — 0.4 | Модель имеет низкую предсказательную способность |
| 0.4 — 0.6 | Модель имеет среднюю предсказательную способность |
| 0.6 — 0.8 | Модель имеет хорошую предсказательную способность |
| 0.8 — 1 | Модель имеет очень высокую предсказательную способность |
Каковы преимущества использования коэффициента детерминации?
1. Оценка точности модели: Коэффициент детерминации позволяет оценить, насколько хорошо модель объясняет вариацию данных. Высокое значение коэффициента детерминации указывает на то, что модель достаточно точно предсказывает зависимую переменную на основе независимых переменных.
2. Сравнение моделей: Коэффициент детерминации позволяет сравнивать различные модели регрессии и выбирать наиболее подходящую. Чем выше значение коэффициента детерминации, тем лучше модель адаптирована к данным и с большей точностью предсказывает результаты.
3. Измерение важности переменных: Коэффициент детерминации также может помочь определить, какие независимые переменные наиболее сильно влияют на зависимую переменную. Если значение коэффициента детерминации для одной переменной высокое, это может указывать на то, что она играет важную роль в предсказании результата.
Обратите внимание, что коэффициент детерминации имеет свои ограничения и не может полностью объяснить всю вариацию данных. Он должен использоваться совместно с другими методами и инструментами для более полного анализа и оценки моделей.
Недостатки использования коэффициента детерминации
2. Неинформативен при сложных моделях: Коэффициент детерминации может быть занижен или завышен при наличии сложных моделей, которые включают в себя множество факторов. Это может привести к неверным интерпретациям и ослабить полезность коэффициента.
3. Не учитывает адекватность модели: Коэффициент детерминации не дает информации о том, насколько хорошо модель описывает данные. Он может быть высоким, но модель все равно может быть непригодной для предсказания новых данных. Поэтому важно проводить дополнительные проверки адекватности модели.
4. Не учитывает динамику данных: Коэффициент детерминации предполагает, что связь между переменными является постоянной и не меняется со временем. Однако, в реальных данных может быть присутствовать динамика, которая не учитывается при расчете коэффициента.
В целом, коэффициент детерминации является полезным инструментом для оценки объяснительной силы модели, но его использование требует осторожности и необходимости учитывать вышеупомянутые недостатки. Необходимо анализировать результаты коэффициента в сочетании с другими статистическими индикаторами для получения полной картины о модели.
Существуют ли альтернативные методы измерения зависимости и предсказания результатов?
Один из таких методов — коэффициент корреляции Пирсона. Он измеряет степень линейной зависимости между двумя переменными. Коэффициент корреляции Пирсона изменяется от -1 до 1, где значение 1 указывает на положительную линейную зависимость, 0 — на отсутствие зависимости, а -1 — на отрицательную линейную зависимость.
Еще один метод — регрессионный анализ. Он позволяет определить математическую модель, которая наилучшим образом подходит для предсказания зависимой переменной на основе независимых переменных. В результате регрессионного анализа можно получить не только коэффициенты уравнения регрессии, но и меру точности модели, такую как среднеквадратичная ошибка.
Также можно использовать машинное обучение и алгоритмы, такие как случайный лес или градиентный бустинг, для предсказания результатов на основе данных. Эти методы могут быть особенно полезны, когда имеется большое количество переменных или когда предполагается нелинейная зависимость.
Таким образом, помимо коэффициента детерминации, существуют альтернативные методы измерения зависимости и предсказания результатов, которые могут быть применены в различных ситуациях в зависимости от специфики данных и поставленных целей исследования.
Влияет ли размер выборки на значение коэффициента детерминации?
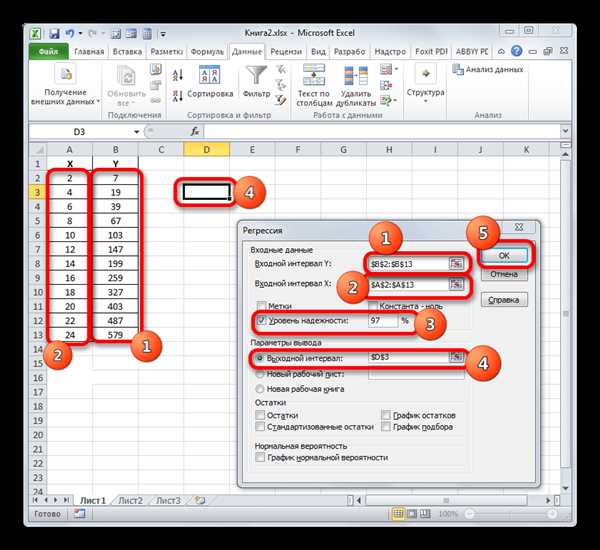
Часто возникает вопрос о том, какой должна быть минимальная выборка, чтобы можно было провести анализ и оценить коэффициент детерминации. Однако, ответ на этот вопрос сложно дать, так как он зависит от множества факторов, включая сложность модели, количество предикторов и уровень желаемой точности оценки.
Тем не менее, существуют некоторые рекомендации. Общепринято считать, что для статистически достоверного оценивания коэффициента детерминации необходимо иметь выборку не менее 30 наблюдений. При этом, по мере увеличения размера выборки, увеличивается точность и надежность оценки коэффициента детерминации.
Однако, следует помнить о том, что качество и интерпретируемость оценки коэффициента детерминации также зависит от других факторов, таких как представительность выборки, правильность выбора модели и правильность предикторов. Также имейте в виду, что ошибочно считать, что большая выборка всегда будет давать более точные результаты. Важно найти правильный баланс между размером выборки и достаточностью данных для анализа.
Какие ошибки могут возникнуть при использовании коэффициента детерминации в Excel?
Применение коэффициента детерминации в Excel может быть полезным при анализе данных и построении регрессионной модели. Однако, при использовании этого показателя могут возникнуть определенные ошибки, которые могут привести к неправильным результатам. Ниже приведены некоторые наиболее распространенные ошибки, которые можно совершить при использовании коэффициента детерминации в Excel:
1. Неправильный выбор переменных
Первой ошибкой может быть неправильный выбор переменных для расчета коэффициента детерминации. Если выбраны неверные переменные или набор данных не достаточно репрезентативен, то это может привести к аналитическим ошибкам. Постарайтесь подобрать переменные, которые имеют высокую корреляцию с зависимой переменной и охватывают широкий диапазон значений.
2. Игнорирование предпосылок
Второй ошибкой может быть игнорирование предпосылок, которые лежат в основе применения коэффициента детерминации. Например, одной из предпосылок является линейная зависимость между переменными. Если эта предпосылка не выполняется, то коэффициент детерминации может быть искажен и использование его результатов может быть неправильным.
3. Использование неправильной формулы
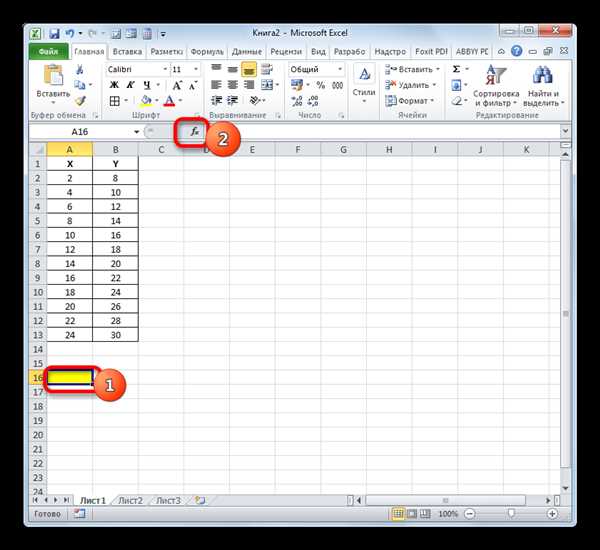
Третьей ошибкой может быть использование неправильной формулы для расчета коэффициента детерминации. В Excel существует несколько функций для расчета коэффициента детерминации, таких как CORREL и RSQ. Важно использовать правильную формулу, иначе расчеты могут быть неправильными.
В целом, при использовании коэффициента детерминации в Excel необходимо быть внимательным и осторожным. Важно правильно выбирать переменные, учитывать предпосылки и использовать правильную формулу для расчета. При соблюдении этих правил, коэффициент детерминации может быть полезным инструментом для анализа и понимания взаимосвязей между переменными.
