Множественный коэффициент корреляции – это статистический показатель, который позволяет определить связь между несколькими независимыми переменными и зависимой переменной. Этот показатель является одним из ключевых инструментов в анализе данных и может быть использован в различных сферах, включая экономику, психологию, медицину и другие.
В программе Excel множественный коэффициент корреляции может быть посчитан с использованием функции MULTIPLE. Эта функция позволяет анализировать данные и определить силу и направление связи между переменными. Для расчета множественного коэффициента корреляции необходимо ввести значения независимых и зависимой переменных в ячейки таблицы и использовать формулу, содержащую функцию MULTIPLE.
Интерпретация множественного коэффициента корреляции в Excel заключается в анализе его значений, которые могут находиться в диапазоне от -1 до 1. Значение -1 означает полную отрицательную связь, значение 1 – положительную связь, а значение 0 – отсутствие связи. Чем ближе коэффициент к 1 или -1, тем сильнее связь между переменными. Значение 0,5 и более считается сильной связью, а значение от 0,3 до 0,5 – умеренной связью.
Множественный коэффициент корреляции Excel
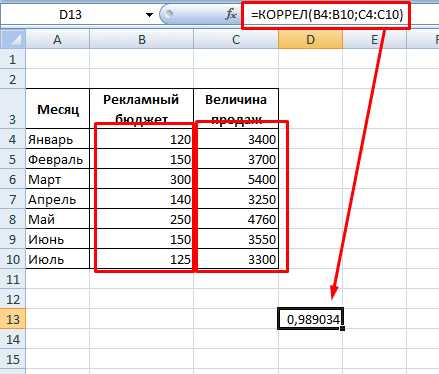
Для рассчета множественного коэффициента корреляции в Excel необходимо воспользоваться функцией CORREL. Данная функция принимает в качестве аргументов массивы или диапазоны данных и возвращает корреляцию между ними.
Процесс расчета множественного коэффициента корреляции в Excel включает в себя следующие шаги:
- Выбор необходимой функции для рассчета коэффициента корреляции (например, функция CORREL).
- Ввод данных во вспомогательные ячейки.
- Написание формулы для расчета коэффициента корреляции.
- Интерпретация полученных результатов.
После расчета множественного коэффициента корреляции в Excel следует проанализировать полученные результаты. Значение коэффициента корреляции может находиться в диапазоне от -1 до 1. Если коэффициент равен 1, это означает, что между переменными существует положительная линейная связь, в то время как значение -1 указывает на наличие отрицательной линейной связи. Значение коэффициента, близкое к нулю, указывает на отсутствие связи между переменными.
Множественный коэффициент корреляции Excel является полезным инструментом для исследования зависимостей между несколькими переменными. Он помогает выявить факторы, оказывающие наибольшее влияние на исследуемую переменную и используется в различных сферах, включая науку, экономику и социологию.
Применение и интерпретация
Применение
Множественный коэффициент корреляции может быть применен для анализа данных в различных областях, таких как экономика, социология, психология и маркетинг. Он позволяет определить степень связи между независимыми переменными и зависимой переменной, а также определить, какие независимые переменные больше всего влияют на зависимую переменную.
Например, предположим, что у нас есть данные о доходе, возрасте и уровне образования людей. Мы можем использовать множественный коэффициент корреляции для определения степени взаимосвязи между этими переменными и предсказывать, как доход зависит от возраста и уровня образования.
Интерпретация
Значение множественного коэффициента корреляции может находиться в диапазоне от -1 до 1. Значение близкое к 1 означает сильную положительную корреляцию, когда значения переменных меняются вместе. Значение близкое к -1 означает сильную отрицательную корреляцию, когда значения переменных меняются в противоположных направлениях.
Кроме того, для оценки статистической значимости коэффициента корреляции используется p-value. Если p-value меньше заданного уровня значимости (обычно 0,05), то мы можем считать корреляцию статистически значимой.
При интерпретации множественного коэффициента корреляции также важно учитывать контекст и специфику исследования. Необходимо учитывать возможные ограничения и предположения модели, а также проводить дополнительные анализы для проверки статистической значимости результатов.
| Значение коэффициента корреляции (r) | Толкование |
|---|---|
| r > 0 | Положительная корреляция |
| r < 0 | Отрицательная корреляция |
| r = 0 | Отсутствие корреляции |
Определение коэффициента корреляции
Множественный коэффициент корреляции — это один из способов расчета коэффициента корреляции, когда необходимо учесть влияние нескольких независимых переменных на зависимую переменную. Он позволяет исследователям определить, какие из независимых переменных вносят наибольший вклад в объяснение изменчивости зависимой переменной.
Формула множественного коэффициента корреляции
Множественный коэффициент корреляции рассчитывается по формуле:
r = v(R2)
где r — множественный коэффициент корреляции, R2 — коэффициент детерминации.
Интерпретация множественного коэффициента корреляции
Множественный коэффициент корреляции принимает значения от -1 до 1. Чем ближе значение к 1 или -1, тем сильнее связь между переменными. Знак коэффициента указывает на направление связи: позитивную (+1) или негативную (-1).
Значение коэффициента близкое к 0 указывает на отсутствие связи между переменными. Чем ближе значение к 0, тем слабее связь.
Интерпретация множественного коэффициента корреляции включает также оценку статистической значимости. P-значение позволяет определить, насколько вероятна случайность связи между переменными. Значение p-значения менее 0,05 обычно считается статистически значимым.
Значение и основы статистики
Основные понятия статистики, которые полезно знать, включают:
- Среднее значение: это сумма всех значений, разделенная на количество значений. Среднее значение помогает понять центральную тенденцию данных.
- Дисперсия: это мера разброса данных относительно их среднего значения. Большая дисперсия указывает на большой разброс данных.
- Стандартное отклонение: это квадратный корень из дисперсии. Стандартное отклонение указывает на среднее расстояние данных от среднего значения.
- Корреляция: это мера силы и направления связи между двумя переменными. Корреляция может быть положительной (оба значения увеличиваются) или отрицательной (одно значение увеличивается, а другое уменьшается).
- Множественный коэффициент корреляции: это статистическая мера, которая показывает силу и направление связи между одной зависимой переменной и двумя или более независимыми переменными.
Понимание этих основных статистических понятий помогает в понимании процесса анализа и интерпретации данных с использованием множественного коэффициента корреляции Excel. Результаты статистического анализа исследуемых данных могут помочь выявить связи и тренды, что может быть полезно для принятия решений и разработки стратегий в различных областях, таких как маркетинг, экономика, социология и другие.
Множественный коэффициент корреляции
Как использовать функцию CORREL
Для расчета множественного коэффициента корреляции в Excel необходимо выполнить следующие шаги:
- Откройте новый документ Excel и создайте две или более переменные, которые будут использоваться для расчета корреляции.
- Выберите ячейку, в которой будет находиться результат расчета.
- Введите формулу =CORREL(range1, range2) в выбранную ячейку, где range1 и range2 представляют собой диапазоны данных для переменных.
- Нажмите Enter, чтобы выполнить формулу и получить значения множественного коэффициента корреляции.
Как интерпретировать множественный коэффициент корреляции
Значение множественного коэффициента корреляции может варьироваться от -1 до 1. Положительное значение указывает на прямую связь между переменными, тогда как отрицательное значение указывает на обратную связь.
Чем ближе значение коэффициента к 1 или -1, тем сильнее связь между переменными. Значение 0 указывает на отсутствие связи. Важно также учитывать статистическую значимость коэффициента при интерпретации результатов.
Пример интерпретации множественного коэффициента корреляции может быть следующим: Множественный коэффициент корреляции составляет 0,8, что указывает на сильную положительную связь между переменными. Значение является статистически значимым на уровне 0,05.
| Значение | Интерпретация |
|---|---|
| От -1 до -0,7 или от 0,7 до 1 | Очень сильная связь |
| От -0,7 до -0,5 или от 0,5 до 0,7 | Сильная связь |
| От -0,5 до -0,3 или от 0,3 до 0,5 | Умеренная связь |
| От -0,3 до -0,1 или от 0,1 до 0,3 | Слабая связь |
| От -0,1 до 0,1 | Отсутствие связи |
Использование множественного коэффициента корреляции в Excel позволяет более точно изучить взаимосвязь между переменными и провести более обоснованный анализ.
Особенности и примеры расчета
Расчет множественного коэффициента корреляции используется для определения силы и направления взаимосвязи между переменными в модели. Он позволяет определить, насколько хорошо модель объясняет вариацию зависимой переменной и предсказывает ее значения на основе наблюдаемых данных.
Пример расчета множественного коэффициента корреляции
Допустим, у нас есть данные о доходе (Y) и количестве отработанных лет (X1) для 50 человек. Мы хотим узнать, есть ли связь между этими переменными и насколько сильна эта связь.
Шаг 1: Загрузка данных в Excel.
- Создайте таблицу с двумя столбцами: один для дохода, другой для количества отработанных лет.
- Заполните значения для каждого человека.
Шаг 2: Вычисление множественного коэффициента корреляции.
- Выделите столбцы с данными.
- Откройте вкладку Данные и выберите Анализ данных.
- Выберите Регрессия и нажмите ОК.
- Введите диапазоны переменных для Ввод данных Y и Ввод данных X.
- Убедитесь, что установлена опция Множественный коэффициент корреляции и нажмите ОК.
Шаг 3: Интерпретация результата.
После выполнения расчетов Excel выдаст множественный коэффициент корреляции. Если значение близко к 1 или -1, это указывает на сильную связь между переменными. Если значение близко к 0, связь считается слабой или отсутствующей.
Например, если множественный коэффициент корреляции равен 0,8, это означает, что 80% вариации дохода может быть объяснено количеством отработанных лет.
Важно помнить, что множественный коэффициент корреляции не дает нам никакой информации о причинно-следственной связи между переменными. Он лишь показывает степень связи и предсказуемость переменных в модели.
Интерпретация коэффициента корреляции
Положительная корреляция
Если значение коэффициента корреляции близко к 1, это указывает на положительную корреляцию. Это означает, что переменные движутся в одном направлении: когда одна переменная увеличивается, другая переменная также увеличивается.
Отрицательная корреляция
Если значение коэффициента корреляции близко к -1, это указывает на отрицательную корреляцию. Это означает, что переменные движутся в противоположных направлениях: когда одна переменная увеличивается, другая переменная уменьшается.
Значение коэффициента корреляции равное 0 указывает на отсутствие линейной связи между переменными. Однако, это не означает, что между ними нет никакой связи, так как может существовать нелинейная зависимость.
При интерпретации результатов множественного коэффициента корреляции необходимо также учитывать его статистическую значимость. Если значение коэффициента корреляции является статистически значимым, то можно считать его более доверительным и надежным.
Как определить силу связи
При использовании множественного коэффициента корреляции в Excel можно определить силу связи между различными переменными. Силу связи можно оценить по значению коэффициента корреляции, который может принимать значения от -1 до 1.
Чем ближе значение коэффициента корреляции к 1 или -1, тем сильнее связь между переменными. Значение 1 означает положительную линейную связь, тогда как значение -1 означает отрицательную линейную связь. Значение 0 означает отсутствие связи.
Если коэффициент корреляции находится в диапазоне от 0 до 0,3, то связь между переменными считается слабой. Если коэффициент корреляции находится в диапазоне от 0,3 до 0,7, то связь между переменными считается умеренной. Если коэффициент корреляции находится в диапазоне от 0,7 до 1 (или от -1 до -0,7), то связь между переменными считается сильной.
При интерпретации коэффициента корреляции, стоит также обратить внимание на величину выборки. Чем больше значений в выборке, тем более точным и надежным будет коэффициент корреляции. При небольшой выборке следует быть осторожным при суждениях о силе связи.
Применение множественного коэффициента корреляции
Установление связи между переменными
Множественный коэффициент корреляции позволяет определить, насколько сильно и каким образом зависит зависимая переменная от независимых переменных. Значение коэффициента может варьировать от -1 до 1. Если коэффициент равен 0, то это указывает на отсутствие связи между переменными.
Важно понимать, что коэффициент корреляции не указывает на причинно-следственную связь между переменными, а только на существование связи. При выполнении множественного регрессионного анализа можно получить уравнение, которое позволяет оценить вклад каждой независимой переменной в объяснение зависимой переменной.
Интерпретация коэффициента корреляции
Значение множественного коэффициента корреляции варьируется от -1 до 1. Положительное значение коэффициента указывает на прямую связь между переменными, то есть увеличение одной переменной приводит к увеличению другой. Отрицательное значение коэффициента указывает на обратную связь между переменными, то есть увеличение одной переменной приводит к уменьшению другой.
Чем ближе значение коэффициента корреляции к 1 или -1, тем сильнее связь между переменными. Значение коэффициента, близкое к 0, указывает на отсутствие связи между переменными.
Важным аспектом интерпретации коэффициента корреляции является его статистическая значимость. Значение p-value позволяет определить, насколько достоверна полученная связь между переменными. Если значение p-value меньше заданного уровня значимости (обычно 0,05), то можно считать связь статистически значимой.
В анализе экономических данных
МКК в Excel можно рассчитать с помощью специальной функции CORREL, которая позволяет вычислить коэффициент корреляции между двумя или более переменными. Однако для расчета МКК в Excel необходимо использовать дополнительные инструменты, такие как анализ регрессии или инструменты анализа данных.
Интерпретация МКК в экономическом анализе может быть сложной задачей. Во-первых, МКК может принимать значения от -1 до 1. Значение 1 означает идеальную положительную линейную связь между переменными, в то время как значение -1 означает идеальную отрицательную линейную связь. Значение близкое к 0 указывает на отсутствие связи между переменными.
Все промежуточные значения между -1 и 1 могут указывать на различные степени и направления связи между переменными. Например, значение 0,7 означает достаточно сильную положительную связь, в то время как значение -0,4 указывает на слабую отрицательную связь.
Однако важно помнить, что коэффициент корреляции не означает причинно-следственную связь между переменными. Он лишь показывает наличие связи и ее характер, но не указывает на то, что одна переменная вызывает изменение другой.
В анализе экономических данных МКК является полезным инструментом, который помогает выявить взаимосвязь между переменными. Правильная интерпретация МКК может помочь в принятии более информированных решений в экономической сфере.
Множественный коэффициент корреляции и регрессия
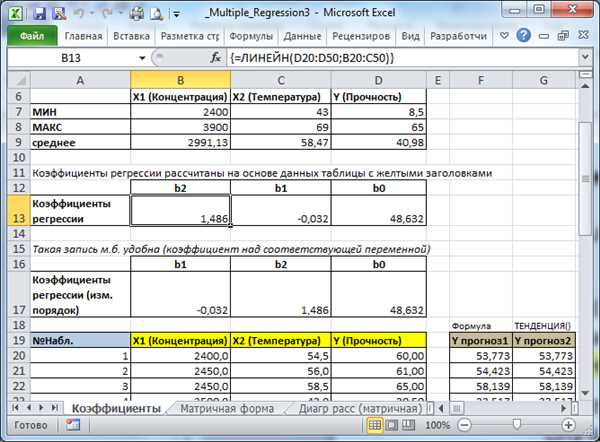
Множественный коэффициент корреляции (R-квадрат) представляет собой меру силы и направления связи между зависимой переменной и независимыми переменными. Значение R-квадрат лежит в диапазоне от 0 до 1, где 0 означает отсутствие связи, а 1 — идеальную связь.
Множественная регрессия используется для построения модели, которая предсказывает значения зависимой переменной на основе значений одной или нескольких независимых переменных. Эта модель позволяет исследователям оценить вклад каждой независимой переменной в объяснение изменений зависимой переменной и сделать прогнозы.
Интерпретация результатов
При интерпретации множественного коэффициента корреляции и регрессии необходимо обратить внимание на следующие аспекты:
- Значение R-квадрат: ближе значение к 1, тем сильнее связь между переменными.
- Значимость коэффициентов: это показатель того, насколько статистически значимы коэффициенты регрессии.
- Направление и сила связи: положительное направление связи означает, что с ростом значений независимых переменных, зависимая переменная также увеличивается.
- Практическая значимость: помимо статистической значимости, необходимо также оценить практическую значимость влияния независимых переменных на зависимую переменную.
Важно помнить, что множественный коэффициент корреляции и регрессия не могут подтвердить причинно-следственную связь между переменными, а только показать наличие связи и ее степень.
Соотношение между показателями
Множественный коэффициент корреляции в Excel позволяет определить силу и направление связи между несколькими переменными. Он позволяет оценить, насколько хорошо одна или несколько независимых переменных предсказывают зависимую переменную. Соотношение между показателями может быть положительным, отрицательным или нулевым.
Положительное соотношение означает, что две или более переменные движутся в одном направлении. Например, если повышение стоимости рекламы приводит к увеличению продажи товаров, это положительное соотношение. В этом случае, увеличение одной переменной сопровождается увеличением другой переменной.
Отрицательное соотношение означает, что две или более переменные движутся в противоположных направлениях. Например, если увеличение цены товара приводит к снижению спроса, это отрицательное соотношение. В этом случае, увеличение одной переменной сопровождается снижением другой переменной.
Нулевое соотношение означает, что между переменными нет связи. Изменение одной переменной не влияет на другую переменную. Например, если предсказываемая переменная (продажи) не зависит от никаких независимых переменных (цена, реклама), то соотношение между ними будет нулевым.
Знание о соотношении между показателями помогает анализировать данные и принимать решения на основе их взаимосвязи. Множественный коэффициент корреляции в Excel предоставляет инструмент для измерения и интерпретации этого соотношения, позволяя исследователям и бизнес-аналитикам прогнозировать и предсказывать результаты в зависимости от изменения независимых переменных.
Ошибки и ограничения при использовании коэффициента корреляции
Вот некоторые из наиболее распространенных ошибок, которые могут возникнуть при интерпретации коэффициента корреляции:
| Ошибка | Описание |
|---|---|
| Случайная корреляция | Коэффициент корреляции может быть значимым только на уровне вероятности. Он не дает информацию о причинно-следственных связях, и случайные корреляции могут быть ошибочно истолкованы как причинно-следственные связи. |
| Выборочный коэффициент корреляции | Коэффициент корреляции, рассчитанный на основе выборки, может отличаться от истинного значения коэффициента корреляции в генеральной совокупности. |
| Обратное взаимодействие | Множественный коэффициент корреляции может не улавливать сложные взаимосвязи между переменными, такие как обратное взаимодействие. |
| Непропорциональность вкладов | Множественный коэффициент корреляции может не отражать непропорциональность вкладов переменных в объяснение дисперсии в зависимой переменной. |
Имея в виду потенциальные ошибки и ограничения, связанные с использованием множественного коэффициента корреляции, важно осуществлять тщательный анализ и предпринимать дополнительные шаги для проверки защищенности результатов.
